“The Milky Way is nothing else but a mass of innumerable stars planted together in clusters.” – Galileo Galilei
“은하수는 별게 아니고 셀 수 없이 많은 별들이 한데 모여있는 것이다.” – 갈릴레오 갈릴레이

화학에는 사람 이름을 딴 법칙들이 꽤 있다. 화학의 기본적인 법칙 중 하나인 아보가드로 법칙도 그 예다. 위의 그림이 이 법칙(또는 가설)을 처음 세운 아메데오 아보가드로라는 과학자다. 이름이 해괴해서 그렇지 법칙 자체는 생각보다 간단하다. “기체의 종류에 관계 없이, 같은 온도와 같은 압력 조건에서는, 같은 부피 속에 들어 있는 기체 입자의 개수는 일정하다”는 것이 그 내용이다. 물론 세상이 그렇게 단순한 건 아니었고, 과학 측정 기술이 발달하면서 실제로 기체의 종류에 따라 개수가 조금씩 달라진다. 하지만 그렇다고 큰 아이디어까지 부정할 필요는 없다. 대체로 같은 부피의 기체 속에는 같은 수의 입자가 있다고 봐도 무방하다는 것이다. 기체의 종류도 상관이 없다. 즉, 기체의 부피에 영향을 주는 요소는 크게 세 가지 (압력, 온도, 기체 입자 개수) 밖에 없는 것이라고 상황을 단순화할 수 있다는 것이 이 법칙의 유용함이다.

그러면 어떻게 이런 극단적으로 단순한 법칙이 대강이나마 맞아 들어갈 수 있을까? 그 실마리는 기체라는 물질의 상태를 살펴봄으로써 찾을 수 있다. 물질은 보통 고체, 액체, 기체의 세 가지 상태로 존재한다. 고체가 입자들이 질서정연하게 서로 연결된 상태라면, 액체는 중간 중간에 끊어진 부분이 있는 것이고, 기체는 입자들이 전부 제멋대로 돌아다니는 상태라고 볼 수 있다. 온도가 높아지면서 고체가 녹아 액체가 되면, 입자들이 질서 정연하게 있다가 부분적으로만 뭉쳐있게 되면서 부피가 증가한다. 이 때 증가하는 정도라고 해봐야 거의 눈에 띄지 않는다. 하지만 액체가 기체로 변할 때는 부피가 거의 1000배 가까이 증가하게 된다. 모든 입자가 완전히 자유롭게 알아서 날뛰는 상태기 때문이다. 고체는 군기가 강하게 잡힌 군인들, 액체는 군기 빠진 상태, 기체는 당나라 군대라고 보면 된다. 따라서, 물질은 기체가 되는 순간 “부피”라는 측면에 있어서는 개개의 입자의 특성이 별로 상관이 없게 된다. 입자 자체가 무겁든 가볍든 크든 작든 날뛰는 정도는 거의 동일하기 때문이다.
그렇다면 압력과 온도가 같을 때 부피와 기체 입자 개수가 비례하는 것은 사실이라 놓았을 때, 실제로 1L 부피의 기체 안에는 입자가 몇 개 들어 있을까? 당연히 한 두개 들어 있는 정도는 아니다. 어렸을 때 배웠던 큰 단위의 수를 세는 몇 억, 몇 조, 몇 경 등의 단위로 서술하기에도 입자의 개수는 너무 많다. 여기에서 새로운 단위가 하나 등장한다. 몰(mole, 단위로 쓸 때는 mol)이 그것이다. 1몰은 탄소 12g에 들어있는 탄소 원자의 개수로 정의된다. 이건 또 뭔 헛소리인가. 그 개수가 얼마인지 궁금한 것인데 말이다. 정의는 정의고, 보통은 1몰은 6.02X10^23개 (0이 23개 있는 수)를 세는 것이라고 생각해 두어도 여태까지 시험보고 살면서 별 지장은 없었다. 이 “몰”이라는 단위는 화학에서 상당히 많이 쓰이는 단위다. 셀 수 없을만큼 많은 수의 분자의 개수를 손쉽게 표현해 주기 때문이다. 조기 스무 마리 엮어 놓은 것을 한 두름이라고 부르는 것 처럼, 6.02X10^23개를 1몰이라고 생각하자. 이상기체식에 따르면 일상적인 온도와 압력에서 22.4L의 부피 안에 1몰의 기체 입자가 들어 있다.
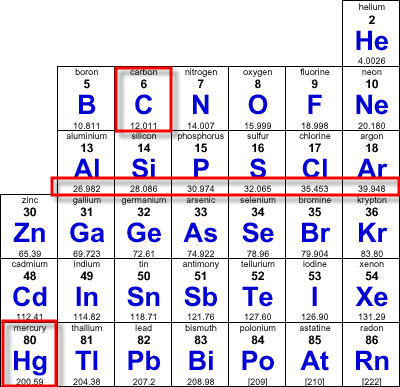
주기율표를 보면 원자마다 원자량이라는 숫자가 함께 적혀있다. 위에서 “몰”의 정의를 이야기 할 때, 12g의 탄소 속에 1몰의 탄소 원자가 들어 있다고 했다. 즉, 원자량은 그 원자를 1몰만큼 모았을 때 질량이 몇 g이나 나가는지 써 놓은 것이다. 위의 그림에서 볼 수 있듯이 원자번호가 커짐에 따라서 원자량도 함께 커짐을 알 수 있다. 탄소의 원자량은 12.011, 수은의 원자량은 200.59니까 같은 개수만큼 원자를 모아 놓으면 수은이 탄소보다 약 16배 정도 더 무겁다는 것도 함께 알 수 있다. 탄소의 원자량이 딱 12가 아니고 12.011과 같이 어정쩡하게 되어 있는 이유는 세상에 탄소 원자들 중에 모두 원자량이 딱 12인 것들만 있는 것이 아니라, 가끔 원자량이 13이거나 14인 것들도 존재하기 때문이다. 12.011이라는 값은 이런 서로 다른 원자량들을 존재 비율을 가중치 삼아서 평균값을 구해서 나온 것이다.

이제 원래의 질문으로 돌아가보자. 아보가드로 법칙에 따라서 22.4L짜리 풍선 속에는 딱 1몰 만큼의 입자(분자 또는 원자)가 들어 있다. 풍선이 헬륨 풍선이든, 자전거 펌프로 바람을 넣은 풍선이든, 입으로 불어서 만든 이산화탄소 풍선이든, 심지어 수은 증기로 만든 풍선이든 종류는 상관 없는 것이다. 헬륨 풍선이라면 22.4L 속에 헬륨 원자가 1몰 들어 있을 것이고, 수은 풍선이면 수은 원자가 1몰 들어 있을 것이다. 온도와 압력이 일정하면 기체의 부피는 입자의 개수와 비례하므로, 1L 풍선 안에는 1/22.4몰만큼의 입자가 들어 있을 것이다. 즉, 약 3X10^22개의 입자가 1L의 풍선 속에는 들어 있는 것이다. 평상시에 쓰는 말로하면 300해개만큼의 헬륨 원자가 1L 헬륨 풍선 안에 들어 있는 것이다. 지구에 있는 모래알 개수를 센 기록이 있는지 모르겠지만, 1L의 풍선 안에 든 기체 입자 개수가 그에 필적할 것이라는 생각은 든다.